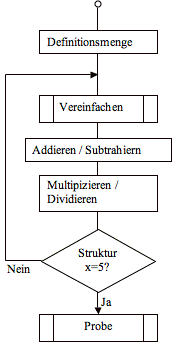
Ablauf als Flussdiagramm
www.ingo-bartling.de
Übungsaufgaben | Wiederholung: Auflösen von Klammern
Mit Klick auf die untere Schaltfläche kann eine Seite mit Übungen erzeugt werden, die man ausdrucken kann. Verwendet werden dabei die aktuellen Optionen (Schwierigkeitsgrad und Klammertypen). Unter den Übungsaufgaben erscheinen die Lösungen. Das Programm erzeugt die Gleichungen und Terme mithilfe eines an vielen Stellen im Prozeß aufgerufenen Zufallsgenerators. Es werden daher jedesmal verschiedene Aufgaben erzeugt!
Eine Gleichung ist ein mathematischer Ausdruck: Beide Seiten links und rechts
des Gleichheitszeichens haben den selben Wert:
1. Bsp.: 5·(4 – 2) = 7 + 3
In Gleichungen können auch Größen vorkommen, deren Wert zunächst nicht bekannt
ist. Es gilt aber, ihren Wert so zu bestimmen, daß die Gleichung wieder
"stimmt", d.h.: links und rechts ergibt sich derselbe Wert. Für diese unbekannte
Größe(n) verwendet man Buchstaben, meist das x, aber auch jeder andere Buchstabe
kann verwendet werden.
2. Bsp.: 5·(x – 2) = 7 + 3
Aus dem 1. Bsp. sieht man: Wenn man statt x die Zahl 4 schreibt, so ergibt die linke Seite der Gleichung den richtigen Wert 10. Man findet übrigens keine andere Zahl, die man für x einsetzen kann, um links insgesamt auf den Wert 10 zu kommen. Die "richtige" Lösung für x ist also die 4. Man schreibt die Lösungsmenge auf: |L={4} oder noch einfacher x=4.
Bei einfachen Gleichungen wie der aus dem Beispiel kann man die Lösung noch
leicht durch Ausprobieren herausfinden. Bei komplizierteren Gleichungen, oder wenn
die Lösung nicht ganzzahlig ist, wird das rasch schwieriger:
3. Bsp.: 4(y – 3) – 2y = 5(–3y + 1)
Es gibt jedoch Verfahren, die Gleichung so umzuformen, daß man den Wert für die unbekannte Größe direkt ablesen kann. Die Voraussetzung für diese Umformungen ist, daß sie die "Gleichheit" der Gleichung, also ihren "Wahrheitsgehalt", nicht verändern.

Ablauf als Flussdiagramm
www.ingo-bartling.de
Kehren wir zum ersten Beispiel zurück. Der erste Schritt besteht immer darin, die Ausdrücke rechts und links so weit zu vereinfachen, wie es geht. Dazu gehört das Auflösen von Klammern (Ausmultiplizieren und/oder Minusklammern) und das Zusammenfassen gleichartiger Summanden (Zahlen und Variablen):
5·(x – 2) = 7 + 3 | Ausmultiplizieren bzw. Ausrechnen 5x – 10 = 10
Dasselbe mit dem zweiten Beispiel:
4(y – 5) – 2y + 8 = 5(–3y + 1) | Ausmultiplizieren auf beiden Seiten 4y – 20 – 2y + 8 = –15y + 5 | Zusammenfassen von Zahlen und Variablen (Umsortieren, Anwendung des Kommutativgesetzes) 4y – 2y – 20 + 8 = –15y + 5 | Ausrechnen 2y – 12 = –15y + 5
Hier gibt es Hilfe zum Auflösen von Klammern.
So weit, so gut.
Die nächsten Schritte bestehen darin, die Gleichung so umzuformen, daß auf einer Seite nur noch
die Variable (x oder y) steht, auf der anderen nur noch eine Zahl. Dann kann man den Wert der
Variablen direkt ablesen.
Hierzu können alle "störenden" Elemente (Summanden und Faktoren) beseitigt, d.h. besser gesagt auf die andere Seite der Gleichung gebracht werden, indem man auf beiden Seiten der Gleichung eine Operation anwendet, die den störenden Summanden oder den störenden Faktor verschwinden läßt.
Bei der Gleichung 5x – 10 = 10 stört zunächst das "– 10" auf der linken Seite. Ein Minus von 10 kann durch ein Plus von 10 beseitigt werden. Vorsicht: Die Gleichung stimmt nur dann weiterhin, wenn man auf beiden Seiten dasselbe verändert:
5x – 10 = 10 | Addieren von 10 5x – 10 + 10 = 10 + 10 | Ausrechnen 5x = 20
Nun "stört" noch der Faktor 5 vor dem x, den man durch Teilen durch 5 beseitigen kann. Vorsicht: Immer beide Seiten der Gleichung gleich behandeln!
5x = 20 | Teilen durch 5 5x/5 = 20/5 | Ausrechnen x = 4
Vorsicht: Beim Teilen und Multiplizieren eines Termes (Rechenausdrucks) müssen alle Summanden durch die Zahl geteilt oder mit ihr multipliziert werden!
Der Zwischenschritt vor dem Ausrechnen kann natürlich entfallen, denn man weiß, daß 10+10 gleich 20 ist.
Die jeweilige Umformung wird rechts von der Gleichung durch den entsprechenden mathematischen Ausdruck vermerkt. Die korrekte Lösung der Gleichung sieht so aus:
5(x – 2) = 7 + 3 | V (Vereinfachen) 5x – 10 = 10 | + 10 5x = 20 | :5 x = 4
Beim zweiten Beispiel geht es so:
4(y – 5) – 2y + 8 = 5(–3y + 1) | V 4y – 20 – 2y + 8 = –15y + 5 | V 2y – 12 = –15y + 5 | + 12 2y = –15y + 17 | + 15y 17y = 17 | : 17 y = 1
Um das Resultat zu überprüfen, überprüft man, ob die Ausgangsgleichung aufgeht, wenn man
für die Variable den herausgefundenen Wert einsetzt: In der Gleichnung
4·(–4) – 2 + 8 = 5·(–2) –16 + 6 = –10 –10 = –10
Dies ist eine wahre Aussage, damit stimmt die Lösung y=1.
Nicht alle Umformungen sind erlaubt, jedoch alle Additionen und Subtraktionen, sowie alle Multiplikationen und Divisionen mit/durch Zahlen ungleich 0.
Ein störendes negatives Vorzeichen vor der Variablen am Ende der Umformungen, z.B. bei -x = 5, kann man durch eine Multiplikation mit (-1) umkehren:
-x = 5 | ·(-1) x = -5
Entsteht am Ende eine Gleichung, in der die Variable nicht mehr vorkommt, so ist die Lösungsmenge leer (|L = Æ), falls diese Gleichung falsch ist (z.B.: 2 = 3). Wenn die Gleichung wahr ist (z.B.: 1 = 1), dann ist die Lösungsmenge gleich der Menge der reellen Zahlen |L = |R.
Das Verfahren zur Auflösung von Klammern hängt vom Rechenzeichen ab, das vor der Klammer steht.
Klammern, vor denen direkt ein Plus-Zeichen steht, können einfach weggelassen werden:
| 5x + (11 – 3x) |
| = 5x + 11 – 3x |
Klammern, vor denen ein Minus steht, werden so behandelt:
Das Minuszeichen und die Klammern
entfallen, dafür werden alle Vorzeichen in der Klammer umgedreht.
1. Bsp.: 4x – (5 + 3x – 7y) = 4x – 5 – 3x + 7y = x + 7y – 5
2. Bsp.: 3x – 36 – (–x2 + 23 – 71x) = 3x – 36 + x2 – 23 + 71x = x2 + 74x - 59
3. Bsp.: –(4x – 4) – (–3x – 5) = –4x + 4 + 3x + 5 = –x + 9
Steht vor der Klammer ein Faktor, so wird beim Auflösen der Klammer jeder Summand in der Klammer mit diesem Faktor
multipliziert. Vorzeichenregeln sind dabei:
(+)·(+) = (+)
(+)·(–) = (–)
(–)·(+) = (–)
(–)·(–) = (+)
1. Bsp.: 5·(x – 2) = 5x – 10 (Der Multipl.-Punkt kann entfallen)
2. Bsp.: –3(5x + 2y) = –15x – 6y
3. Bsp.: 4x(–2 + 3x) = –8x + 12x2
4. Bsp.: –17a(–2b + 3c – 1) = 34ab – 51ac + 17a
Beim Ausmultiplizieren zweier Klammern müssen alle Summanden der ersten Klammer mit allen Summanden
der zweiten Klammer multipliziert werden. Vorzeichen beachten!
1. Bsp.: (a + b)·(c + d) = ac + ad + bc + bd
2. Bsp.: (2 - 3x)(5x + 7) = 10x + 14 – 15x2 – 21x
3. Bsp.: (3a – 11b + 2)(5x – 7) = 15ax – 21a – 55bx + 77b + 10x – 14
4. Bsp.: (a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2 (1. binomische Formel)
5. Bsp.: (a - b)2 = (a – b)(a – b) = a2 – ab – ab + b2 = a2 – 2ab + b2 (2. binomische Formel)
6. Bsp.: (a + b)(a – b) = a2 – ab + ab – b2 = a2 – b2 (3. binomische Formel)
Hierbei empfiehlt sich die Anwendung der Regel "Punkt- vor Strichrechnung", d.h. es
wird zuerst multipliziert und dann erst subtrahiert. Dazu muß jedoch der gesamte Multiplikationsausdruck
in Klammern gesetzt werden, denn der Gültigkeitsbereich des Minuszeichens muß ja erhalten bleiben:
1. Bsp.: –(3 + x)·2 = –[(3 + x)·2)] = –[6 + 2x] = –6 – 2x
Ausdrücke der Form (a + b)² kann man auflösen, ohne das Quadrat auszuschreiben: (a + b)(a + b),
auszumultiplizuieren: a² + ab + ab + b² und zusammenzufassen: a² + 2ab + b², wenn man
das zusammengefaßte Ergebnis a² + 2ab + b² kennt und auf die Summanden in der Klammer
anwendet: (a + b)² = a² + 2ab + b²
a steht dabei für den ersten Summanden in der Klammer und b für den zweiten.
1. Bsp.: (x + 3)² = x² + 2·x·3 + 9 = x² + 6x + 9
2. Bsp.: (2a + 5bx)² = 4a² + 20abx + 25b²x²
Hier ergibt das Ausmultiplizieren von (a - b)(a - b) = a² - ab - ab + b² = a² - 2ab + b².
Auch das kann als Blaupause zum direkten Auflösen der Quadratklammer verwendet werden.
1. Bsp.: (3p — q)² = 9p² — 6pq + q²
2. Bsp.: (7x³ - 3xyz)² = 49x6 - 42x4yz + 9x²y²z²
Beim Ausmultiplizieren und Zusammenfassen stellt sich heraus, daß in diesem Fall der nichtquadratische
Summand verschwindet: (a + b)(a — b) = a² - ab + ab - b² = a² - b².
1. Bsp.: (3x + 0,5)(3x — 0,5) = 9x² - 0,25
2. Bsp.: (6a — 2b)(2b + 6a) = 36a² - 4b²
Im 2. Beispiel wurde das Kommutativgesetz
zweimal angewendet: Die Klammer mit dem Minus steht vorne (Multiplikation ist kommutativ)
und die Summanden in der zweiten Klammer sind vertauscht (Addition ist kommutativ).
Beachte, daß sich die Reihenfolge im Ergebnis nach der Klammer mit dem Minus richtet!
Quelle: Helmut Postel: Aufgabensammlung zur Übung und Wiederholung.
Hannover: Schroedel, 1998.
Nr. 1
|
Nr. 2
|